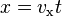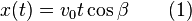One of the elements of Chinese street culture is the habit of spitting. Of course, I will not discuss here the purpose of spitting, or even whether it is right or wrong to spit. All which is covered in my humble mission, is to transfer knowledge and make increase the technical abilities in China. Spitting is not excluded from that. And I do not distinguish whether I personally like it or not. My duty is to make you spit better! One limitation, that I have to acknowledge, is that I have no practical experience in spitting myself and also no plan to gain any. So, please take my lines as a purely theoretical contribution.
Below comes all the tools needed not just to maximise spitting range by optimizing launch speed and angle, but also enables us to calculate how much time we have to step aside after spitting vertically upwards at 90 degrees, not to spit on yourselves. That's cool, just to step away 1/10 second before the impact. Let's go.
Neglecting air drag, in horizontal direction the saliva follows Newton's first law and flies as constant velocity.
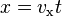
and in vertical direction the saliva is constantly accelerated downward by gravitation

Integration over time derives the vertical location to be

which is nothing else but the commonly known free fall equation.
The x-component of the saliva given the launch velocity (speed of projectile when leaving the mouth) and the launch angle, is
Further the vertical component is

The vectorial equation of the trajectory then follows to be
and the explicit form can be derived by solving Eq. 1 for t and substituting t in Eq. 2:

To estimate the location and the maximum height of the saliva on the trajectory, follows

and

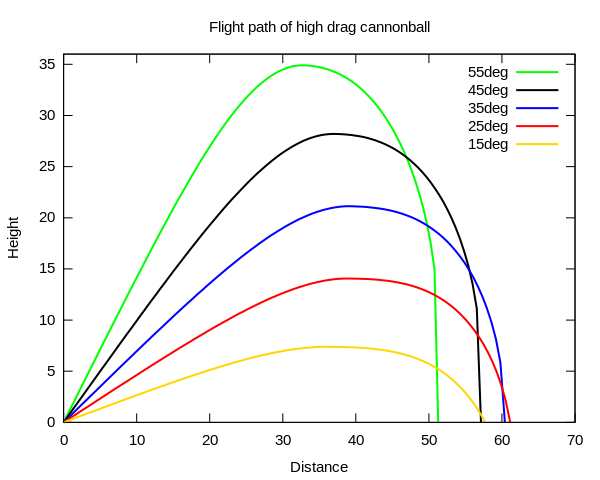
The mathematical descriptions become more complex, if you include the air drag breaking down the aliver speed and changing twisting the trajectory away from parabolic shape, like illustrated below (picture from Wikipedia on artillery projectiles).
Similar processes take place when spitting against the wind and when spitting under strong side wind conditions. This is a field of further research, which I will follow up in future contributions.